Application

There are 2 important and useful rules. One is known as Sine rule and the other is known as Cosine rule.

Here they are:

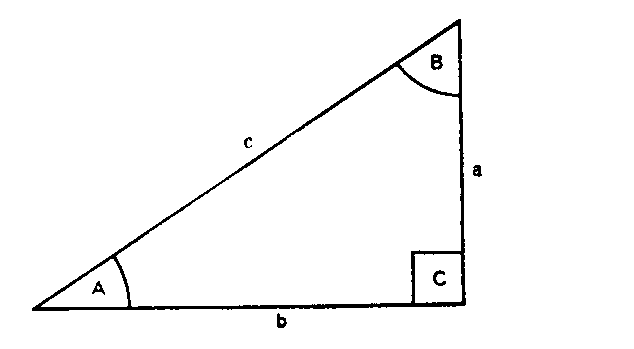
For a given triangle below:

Sine rule:

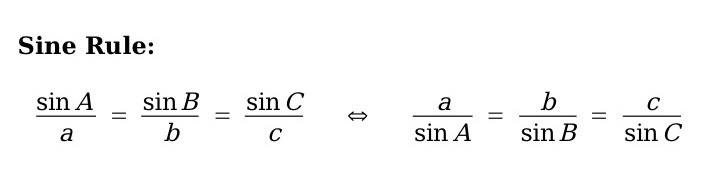
Cosine rule:

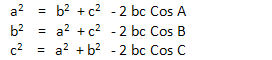
Note that the angles are directly opposite to the sides. For example sin A and side a are directly opposite. 

Here are the proofs - these should help you understand things a little more!

Consider a vertical line that is perpendicular from point B to D.

Let the length of the line be height (h) and;

Let the distance from A to D be x and hence DC is b-x

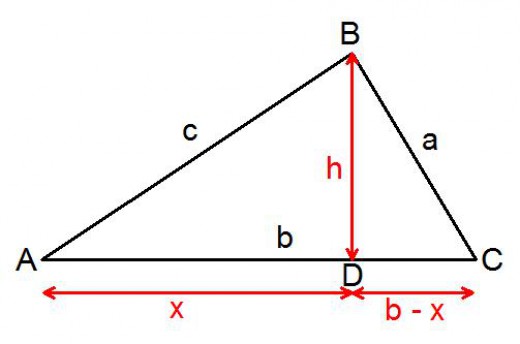
Sine rule:

from the diagram above

sin A = h / c

thus h = c.sin A

and

sin C = h / a

thus h = a.sin C

then since both relationships are equal to h we can say

c.sin A = a.sin C

therefore

sin A / a = sin C / c

Cosine rule:

Then, using Pythagorean Theorem:

(b-x)² + h² = a²

and x² + h² = c²  --> h² = c² - x²

then, sub h² = c² - x² into the first equation we get

(b-x)² + c² - x² = a²

expanding the bracket gives

b² - 2bx + x² + c² - x² = a²

x² cancels out and we are left with

b² - 2bx + c² = a²

Now from the diagram, 

cos A = x / c

then x = c cos A

now substitute this into b² -2bx + c² = a² gives

a² = b² - 2bc.cosA + c²

rearranging gives

a² = b² + c_² -2bc.cosA

This is the cosine rule!