Examples: How Do I Use it?
Write it down as an equation:
a2 + b2 = c2
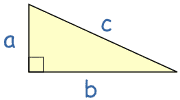
Now you can use algebra to find any missing value!
Example 1: Find the length of c in the following diagram:
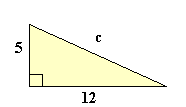
Solution: First, it is important to recognise that side c is the hypotenuse of the triangle. We know this because it is the side opposite the right angle. Therefore, when applying Pythagoras, the sum of the squares of the two known sides must equal the square of c. With this in mind:
a2 + b2 = c2
52 + 122 = c2
25 + 144 = c2
169 = c2
c2 = 169
c = √169
c = 13
Example 2: Find the length of x in the following diagram:
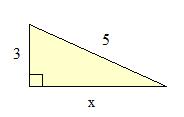
Solution: In this question, it is immediately clear that x is not the hypotenuse of the triangle. Instead, the side of length 5 is the hypotenuse (since it is opposite the right angle). Therefore, we must use the Pythagorean Theorem a little differently. We know that:
x2 + b2 = c2
Therefore, from the diagram above:
x2 + 32 = 52
So, in order to find the length of x, all we need to do is rearrange the above equation in terms of x:
52 - 32 = x2
25 - 9 = x2
16 = x2
x2 = 16
x = √16
x = 4
Check: We know that this answer is right, since the side length that we found was smaller than the hypotenuse. Hooray!
Now I know how to use Pythagoras, where can I use it in everyday life?
Although Pythagoras relates only to triangles, it can be applied to any shape that contains a triangle. This makes it very versatile! Below is just one example of how we can use Pythagoras in the real world!
