Criteria Sheet

The criteria sheet below can be utilised In order to mark students on their performance on the MAPS questions. Simply click on the link to open the file!

Criteria edited.doc (36,5 kB)

Solutions

Pythagorean Theorem

When solving a worded problem, it is important to visualise the situation first. From the information given in the question, we can construct the following diagram:

 So, since the catcher stands at home plate, we need to find the distance from home plate to first base. This distance is represented within the below diagram as x. Also, since the field is a diamond, we know that each corner is exactly 90 degrees - a right angle!

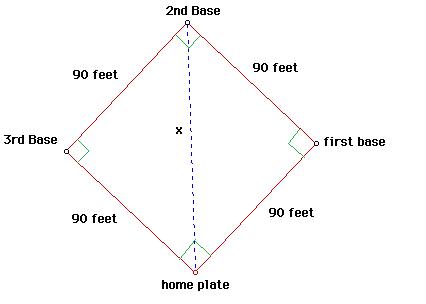
Looking at the above diagram, it is apparent that x is in fact the hypothenuse of a right angle triangle! Using this fact, we can apply Pythagoras to find the length of x.

a² + b² = x²

90² + 90² = x²

16200 = x²

x = 127.2792206

x = 127.28 feet approximately

Therefore, the distance the catcher must throw the ball from home plate to reach second base is approximately 127.28 feet.

Assumptions and Effects

- Assume that all calculations were correct - if this was not the case, the above conclusions would be invalid.

- It was assumed that the catcher was standing at home plate when throwing the ball. If this was not the case (ie the catcher was slightly behind or in front of home plate following a pitch), then the results derived above would be incorrect.

- It was assumed that the bases in the diamond were positioned at exact right angles to each other, an exactly 90 feet apart. If this was not the case, and the positioning was slightly skewed, the use of the Pythagoren Theorem was incorrect, since the triangles created were not right angled. As such, the results derived above would be incorrect.

Trigonometry

The diagram for the MAPS trigonometry problem can be drawn as follows.

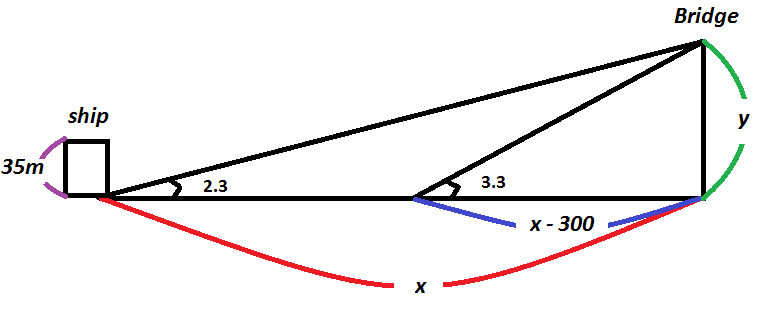
Here we let:

y = height of the bridge

x = current distance from the ship to the bridge

The question asks whether the ship will fit under the bridge or not and the ship is 35m tall. Therefore if y is greater than 35m then the ship will fit.

In other words, we have to calculate the value of y using trigonometry and compare it with the height of ship.

we know that tan of and angle gives opposite / adjacent. Thus, from the diagram using angles we can say:

tan 2.3 = y / x                             rearranging gives y = x tan 2.3

tan 3.3 = y / (x - 300)                  rearranging gives y = (x - 300) tan 3.3

since both equations now equal to y therefore we can let them to be equal, thus:

x tan 2.3 = (x - 300) tan 3.3

x tan 2.3 = x*tan 3.3 - 300*tan 3.3

x tan 2.3 - x tan 3.3 = -300 tan 3.3

x (tan 2.3 - tan 3.3) = -300 tan 3.3

x (0.04 - 0.058) = -17.3

-0.0175x = -17.3

x = -17.3 / -0.0175

x = 988.71m    

but y = x tan 2.3 from above, therefore to work out y

y = 988.71*tan2.3

y = 39.71m

Therefore height of the bridge is taller than height of the ship and thus, the ship will fit under the bridge.

Assumptions:

All measurements are accurate

The bridge forms a right angle with the ocean: If the bridge was not in right angle, then trigonometry theory does not hold.

The surface of the ocean can be described by a straight line: if there were huge waves then this would alter the height of the ship.

Area

Use the formula for the area of a triangle with a given base and height, and create an expression or equation relating the height and base.

The area of a triangle is given by:

A = ( ¹/₂ )bh

...where "b" is the base and "h" is the height (or "altitude"). The height is five less than the base, so the equation for their relationship is:

h = b – 5

Since the area is 52 square inches, plug the base variable, the height expression, and the area value into the formula for the area of a triangle, and see where this leads:

(1/2)(b)(b – 5) = 52 (by substitution for h from the above equation)
b(b – 5) = 104
b² – 5b = 104
b² – 5b – 104 = 0
(b – 13)(b + 8) = 0
b = 13 or b = –8

Safely ignore the extraneous negative solution. (A solution which is "extraneous", pronounced "ek-STRAY-nee-uss", is a number that is a valid solution to the equation, but is not a relevant value in the context of the word problem. In this case, lengths cannot be negative.) This means that b = 13, so h = b – 5 = 13 – 5 = 8.

The base is 13 inches, and the height is 8 inches.